4.5.1. Estadísticas descriptivas
¿Qué es la estadística descriptiva?
La estadística descriptiva es la rama de la estadística que recolecta, analiza y caracteriza un conjunto de datos (peso de la población, beneficios diarios de una empresa, temperatura mensual,…) con el objetivo de describir las características y comportamientos de este conjunto mediante medidas de resumen, tablas o gráficos.

Variables estadísticas
ANUNCIOS
Una variable estadística es el conjunto de valores que puede tomar cierta característica de la población sobre la que se realiza el estudio estadístico y sobre la que es posible su medición. Estas variables pueden ser: la edad, el peso, las notas de un examen, los ingresos mensuales, las horas de sueño de un paciente en una semana, el precio medio del alquiler en las viviendas de un barrio de una ciudad, etc.
Las variables estadísticas se pueden clasificar por diferentes criterios. Según su medición existen dos tipos de variables:
- Cualitativa (o categórica): son las variables que pueden tomar como valores cualidades o categorías.Ejemplos:
- Sexo (hombre, mujer)
- Salud (buena, regular, mala)
- Cuantitativas (o numérica): variables que toman valores numéricos.Ejemplos:
- Número de casas (1, 2,…). Discreta.
- Edad (12,5; 24,3; 35;…). Continua.
Medidas de posición central
Las medidas de tendencia central (o de centralización) son medidas que tienden a localizar en qué punto se encuentra la parte central de un conjunto ordenado de datos de una variable cuantitativa.
Media
Definimos media (también llamada promedio o media aritmética) de un conjunto de datos (X1,X2,…,XN) al valor característico de una serie de datos resultado de la suma de todas las observaciones dividido por el número total de datos.
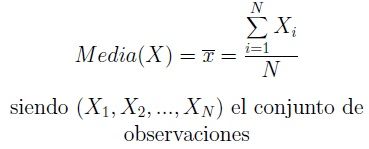
Es decir:


Visto desde un punto de vista más conceptual, la media aritmética es el centro de los datos en el sentido numérico, ya que intenta equilibrarlos por exceso y por defecto. Es decir, si sumamos todas las diferencias de los datos a la media da cero.

Mediana
La mediana (Me(X)) es el elemento de un conjunto de datos ordenados (X1,X2,…,XN) que deja a izquierda y derecha la mitad de valores.

Si el conjunto de datos no está ordenado, la mediana es el valor del conjunto tal que el 50% de los elementos son menores o iguales y el otro 50% mayores o iguales.
Moda
La moda (Mo(X)) es el valor más repetido del conjunto de datos, es decir, el valor cuya frecuencia relativa es mayor. En un conjunto puede haber más de una moda.

Media geométrica
La media geométrica (MG) de un conjunto de números estrictamente positivos (X1, X2,…,XN) es la raíz N-ésima del producto de los N elementos.
Todos los elementos del conjunto tienen que ser mayores que cero. Si algún elemento fuese cero (Xi=0), entonces la MG sería 0 aunque todos los demás valores estuviesen alejados del cero.

Media armónica
La media armónica (H) de un conjunto de elementos no nulos (X1, X2,…,XN) es el recíproco de la suma de los recíprocos (donde 1/Xi es el recíproco de Xi)) multiplicado por el número de elementos del conjunto (N).

Media cuadrática
La media cuadrática o RMS (Root Mean Square) de un conjunto de valores (X1, X2,…,XN) es una medida de posición central. Esta se define como la raíz cuadrada del promedio de los elementos al cuadrado.


Media ponderada
La media ponderada (MP) es una medida de centralización. Consiste en otorgar a cada observación del conjunto de datos (X1,X2,…,XN) unos pesos (p1,p2,…,pN) según la importancia de cada elemento.

Cuanto más grande sea el peso de un elemento, más importante se considera que es éste.
Relación entre medias
Existe una relación de orden entre cuatro tipos de media. En esta relación se excluye la media ponderada porque depende de los pesos. Sean:
- H la media armónica
- MG la media geométrica
- x la media aritmética
- RMS la media cuadrática
Entonces:
En esta relación, solamente se cumple la igualdad cuando todos los datos sean iguales, es decir si: x1 = x2 = x3 = … = xN.
Medidas de posición no central
Las medidas de posición no central (o medidas de tendencia no central) permiten conocer puntos característicos de una serie de valores, que no necesariamente tienen que ser centrales. La intención de estas medidas es dividir el conjunto de observaciones en grupos con el mismo número de valores.
Cuartiles
Los cuartiles son los tres valores que dividen una serie de datos ordenada en cuatro porciones iguales. El primer cuartil (Q1) deja a la izquierda el 25% de los datos. El segundo (Q2) deja a izquierda y derecha el 50% y coincide con la mediana. El tercero (Q3) deja a la derecha el 25% de valores. Los tres cuartiles son:

Percentiles
El percentil es una medida de posición no central. Los percentiles Pi son los 99 puntos que dividen una serie de datos ordenada en 100 partes iguales, es decir, que contienen el mismo número de elementos cada una. El percentil 50 es la mediana.
Sea (X1, X2,…,XN) una muestra de N elementos. El percentil Pi es:

Donde Pi es la posición del percentil buscado en la serie ordenada de datos.
Los percentiles están pensados para conjuntos de elementos de más de cien elementos.
Medidas de dispersión
Las medidas de dispersión o medidas de variabilidad muestran la variabilidad de un conjunto de datos, indicando la mayor o menor concentración de datos respecto a las medias de centralización.
Rango
El rango (R) o recorrido estadístico es la diferencia entre el valor máximo y el mínimo de un conjunto de elementos.
Rango intercuartílico
El rango intercuartílico (IQR) (o rango intercuartil) es una estimación estadística de la dispersión de una distribución de datos. Consiste en la diferencia entre el tercer y el primer cuartil. Mediante esta medida se eliminan los valores extremadamente alejados. El rango intercuartílico es altamente recomendable cuando la medida de tendencia central utilizada es la mediana (ya que este estadístico es insensible a posibles irregularidades en los extremos).

Varianza
La varianza (S2) mide la dispersión de los datos de una muestra respecto a la media, calculando la media de los cuadrados de las distancias de todos los datos.

Al elevar las diferencias al cuadrado se garantiza que las diferencias absolutas respecto a la media no se anulan entre si. Además, resaltan los valores alejados.
Desviación típica
La desviación típica es la medida de dispersión (S) asociada a la media. Mide el promedio de las desviaciones de los datos respecto a la media en las mismas unidades de los datos.

El cuadrado de la desviación típica es la varianza.
Coeficiente de variación de Pearson
El coeficiente de variación de Pearson (r) mide la variación de los datos respecto a la media, sin tener en cuenta las unidades en la que están.

El coeficiente de variación toma valores entre 0 y 1. Si el coeficiente es próximo al 0, significa que existe poca variabilidad en los datos y es una muestra muy compacta. En cambio, si tienden a 1 es una muestra muy dispersa.
Para interpretar fácilmente el coeficiente, podemos multiplicarlo por cien para tenerlo en tanto por cien.
Asimetría y curtosis
La asimetría y curtosis informan sobre la forma de la distribución de una variable. Estas medidas permiten saber las características de su asimetría y homgeneidad sin necesidad de representarlos gráficamente.
Asimetría
La asimetría es la medida que indica la simetría de la distribución de una variable respecto a la media aritmética, sin necesidad de hacer la representación gráfica. Los coeficientes de asimetría indican si hay el mismo número de elementos a izquierda y derecha de la media.
Existen tres tipos de curva de distribución según su asimetría:
- Asimetría negativa: la cola de la distribución se alarga para valores inferiores a la media.
- Simétrica: hay el mismo número de elementos a izquierda y derecha de la media. En este caso, coinciden la media, la mediana y la moda. La distribución se adapta a la forma de la campana de Gauss, o distribución normal.
- Asimetría positiva: la cola de la distribución se alarga para valores superiores a la media.

Curtosis
La curtosis (o apuntamiento) es una medida de forma que mide cuán escarpada o achatada está una curva o distribución.
Este coeficiente indica la cantidad de datos que hay cercanos a la media, de manera que a mayor grado de curtosis, más escarpada (o apuntada) será la forma de la curva.

La curtosis se mide promediando la cuarta potencia de la diferencia entre cada elemento del conjunto y la media, dividido entre la desviación típica elevado también a la cuarta potencia. Sea el conjunto X=(x1, x2,…, xN), entonces el coeficiente de curtosis será:

Frecuencias
La frecuencia es una medida que sirve para comparar la aparición de un elemento Xi en un conjunto de elementos (X1, X2,…, XN). Mediante tablas de distribuciones de frecuencia se puede presentar organizadamente el recuento de datos.
Las frecuencias de cada elemento se pueden expresar tanto absolutas (número total de apariciones) como relativas (proporción de apariciones).
Frecuencia absoluta
La frecuencia absoluta (ni) de un valor Xi es el número de veces que el valor está en el conjunto (X1, X2,…, XN).
La suma de las frecuencias absolutas de todos los elementos diferentes del conjunto debe ser el número total de sujetos N. Si el conjunto tiene k números (o categorías) diferentes, entonces:

Frecuencia absoluta acumulada
La frecuencia absoluta acumulada(Ni) de un valor Xi del conjunto (X1, X2,…, XN) es la suma de las frecuencias absolutas de los valores menores o iguales a Xi, es decir:
Frecuencia relativa
La frecuencia relativa (fi) de un valor Xi es la proporción de valores iguales a Xi en el conjunto de datos (X1, X2,…, XN). Es decir, la frecuencia relativa es la frecuencia absoluta dividida por el número total de elementos N:

Las frecuencias relativas son valores entre 0 y 1, 0 ≤ fi ≤ 1. La suma de las frecuencias relativas de todos los sujetos da 1. Supongamos que en el conjunto tenemos k números (o categorías) diferentes, entonces:

Si se multiplica la frecuencia relativa por cien se obtiene el porcentaje (tanto por cien %).
Frecuencia relativa acumulada
Definimos la frecuencia relativa acumulada (Fi) de un valor Xi como la proporción de valores iguales o menores a Xi en el conjunto de datos (X1, X2,…, XN). Es decir, la frecuencia relativa acumulada es la frecuencia absoluta acumulada dividida por el número total de sujetos N:

La frecuencia relativa acumulada de cada valor siempre es mayor que la frecuencia relativa. De hecho, la frecuencia relativa acumulada de un elemento es la suma de las frecuencias relativas de los elementos menores o iguales a él, es decir:
Gráficos
ANUNCIOS
Un gráfico (o gráfica) es el recurso de representar los datos numéricos por medio de líneas, diagramas, dibujos, etc. La representación gráfica es un importante suplemento al análisis y estudio estadístico.

Los gráficos llaman la atención del lector y hacen que de un vistazo éste tenga una mayor comprensión de los datos. Un buen gráfico puede captar al lector para que a continuación lea todo el estudio. Si un estudio se compone únicamente de texto y tablas, posiblemente no todos los lectores lean el estudio.
Existen muchas clases de gráficas. Se pueden destacar los siguientes tipos:
Gráfico lineal
El gráfico lineal (gráfico de líneas o diagrama lineal) se compone de una serie de datos representados por puntos, unidos por segmentos lineales. Mediante este gráfico se puede comprobar rápidamente el cambio de tendencia de los datos.
El diagrama lineal se suele utilizar con variables cuantitativas, para ver su comportamiento en el transcurso del tiempo. Por ejemplo, en las series temporales mensuales, anuales, trimestrales, etc.

Diagrama
Un diagrama es un tipo de representación gráfica que sirve para representar un conjunto de datos.
Según la RAE (Real Academia Española), un diagrama es un dibujo geométrico que sirve para demostrar una proposición, resolver un problema o representar de una manera gráfica la ley de variación de un fenómeno.
Existen diferentes tipos de diagramas, de los que se pueden destacar los siguientes:
Diagrama de barras
El diagrama de barras es un gráfico que se utiliza para representar datos de variables cualitativas o discretas. Está formado por barras rectangulares cuya altura es proporcional a la frecuencia de cada uno de los valores de la variable.
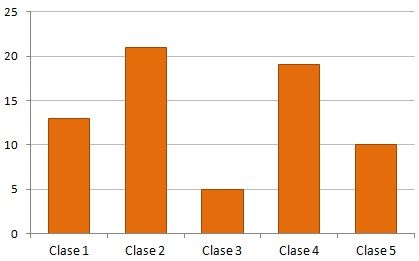
Diagrama circular
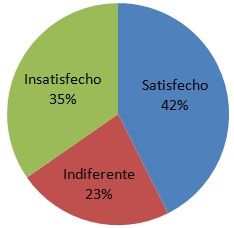
El diagrama circular (también llamado diagrama de sectores o diagrama de pastel) sirve para representar variables cualitativas o discretas. Se utiliza para representar la proporción de elementos de cada uno de los valores de la variable.
Consiste en partir el círculo en porciones proporcionales a la frecuencia relativa. Entiéndase como porción la parte del círculo que representa a cada valor que toma la variable.

Diagrama de Pareto
El diagrama de Pareto (también llamado diagrama ABC) fue creado por Vilfredo Pareto, para representar datos cualitativos. El italiano comprobó que el 20% de la población italiana acaparaban el 80% de riquezas y propiedades.
El principio de Pareto afirma que el 20% de las causas vitales originan alrededor del 80% de los efectos. O visto desde el punto de vista matemático, que el 20% de las categorías representan el 80% de las observaciones.
El diagrama de Pareto se construye siguiendo estos dos pasos:
- Ordenar los datos por frecuencia relativa o absoluta.
- Representar cada una de las categorías de la variable mediante un rectángulo proporcional a su frecuencia (como en el diagrama de barras).

Diagrama de caja
El diagrama de caja es un gráfico utilizado para representar una variable cuantitativa (variable numérica). El gráfico es una herramienta que permite visualizar, a través de los cuartiles, cómo es la distribución, su grado de asimetría, los valores extremos, la posición de la mediana, etc. Se compone de:
- Un rectángulo (caja) delimitado por el primer y tercer cuartil (Q1 y Q3). Dentro de la caja una línea indica dónde se encuentra la mediana (segundo cuartil Q2)
- Dos brazos, uno que empieza en el primer cuartil y acaba en el mínimo, y otro que empieza en el tercer cuartil y acaba en el máximo.
- Los datos atípicos (o valores extremos) que son los valores distintos que no cumplen ciertos requisitos de heterogeneidad de los datos.

Diagrama de tallo y hojas
El diagrama de tallo y hojas (Stem-and-Leaf Diagram) es un semigráfico que permite presentar la distribución de una variable cuantitativa. Consiste en separar cada dato en el último dígito (que se denomina hoja) y las cifras delanteras restantes (que forman el tallo).

Es especialmente útil para conjuntos de datos de tamaño medio (entre 20 y 50 elementos) y que sus datos no se agrupan alrededor de un único tallo. Con él podemos hacernos la idea de qué distribución tienen los datos, la asimetría, etc.

Histograma
Un histograma es una representación gráfica de datos agrupados mediante intervalos. Los datos provienen de una variables cuantitativas continuas. Gracias a él puedes hacerte rápidamente una idea de la distribución de los datos o muestra.
También cabe emplear variables cualitativas ordinales, siendo necesario que el número de datos sea alto.
Un histograma es un conjunto de rectángulos que representan las frecuencias absolutas de cada uno de los intervalos. Los intervalos abarcan todo el conjunto sin cortarse, de manera que un elemento está solo en un intervalo.

Polígono de frecuencias
El polígono de frecuencias es un gráfico que permite la rápida visualización de las frecuencias de cada una de las categorías del estudio.
Normalmente se utiliza el polígono de frecuencias con frecuencias absolutas, pero también se utiliza con frecuencias relativas.

Pictograma
Un pictograma es un tipo de gráfico que representa mediante dibujos la característica estudiada. Éstos representan las frecuencias relativas o absolutas de una variable cualitativa o discreta.

Comentarios
Publicar un comentario